Enrollment

• Understanding Normal Counting

  +

  The way we count, we can have 10 digits in one number place (which you might know if you have learned place value). This means that any number is made up of only the digits 0,1,2,3,4,5,6,7,8, and 9. There are no other “symbols” we use to represent numbers.

  So what happens if we have more than 9 things? How would we show that in our number system? Well then we just start counting from 1 again but we put the 1 in a higher place than the 9. We would put a 1 in the tens place. So that would be 10.

  If this seems confusing, you can look at it shown in a table below. Remember, we only have the digits 0,1,2,3,4,5,6,7,8, and 9 to show any number:

  

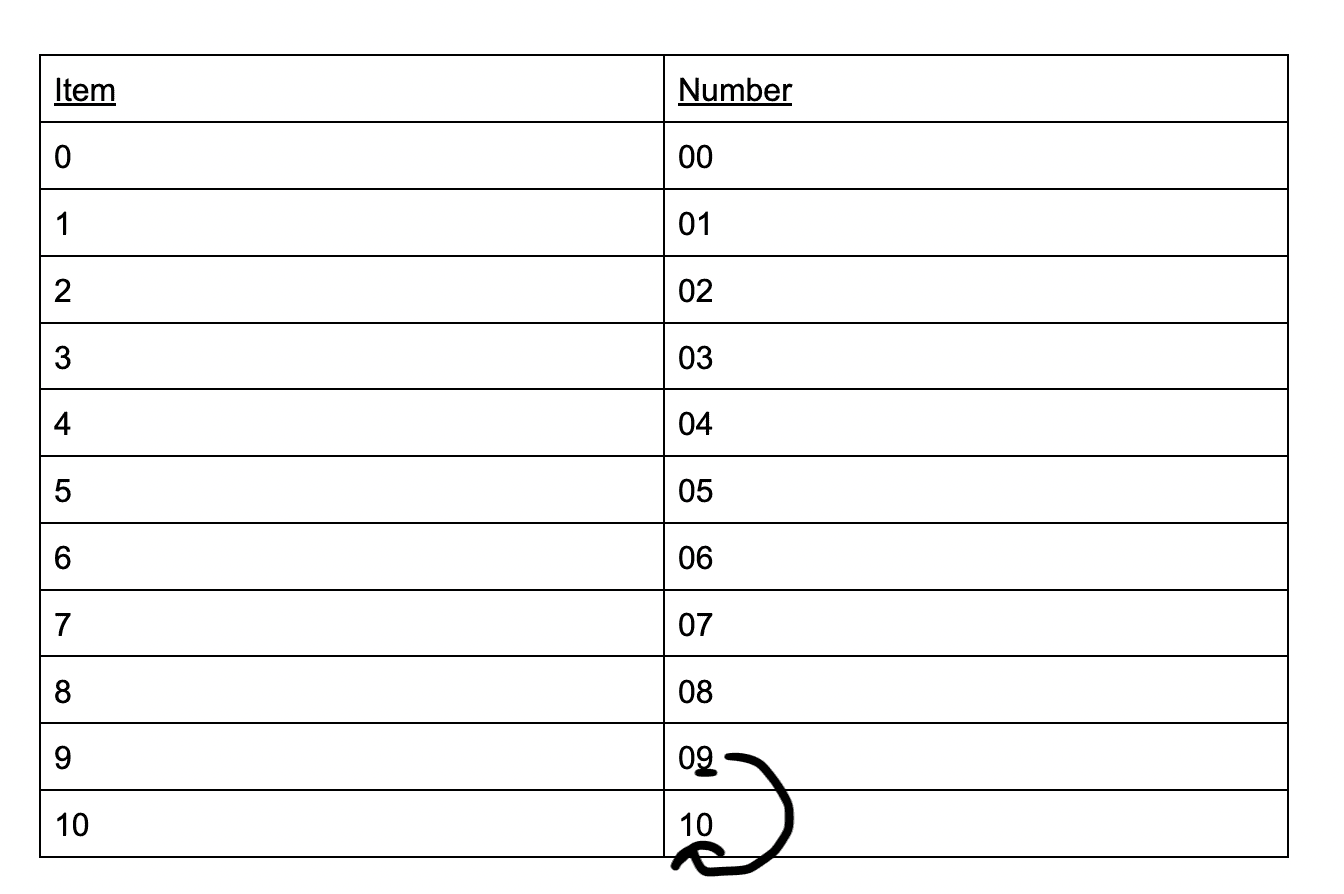
  Look above and notice what happens when we need to show a number that is larger than 9. We don’t have any bigger symbols or digits to show. So, we start counting from 1 again, but we change the position of the 1. When there are not enough symbols/digits to show a certain number, we add a position on the left and start counting from there until we reach our number:

  

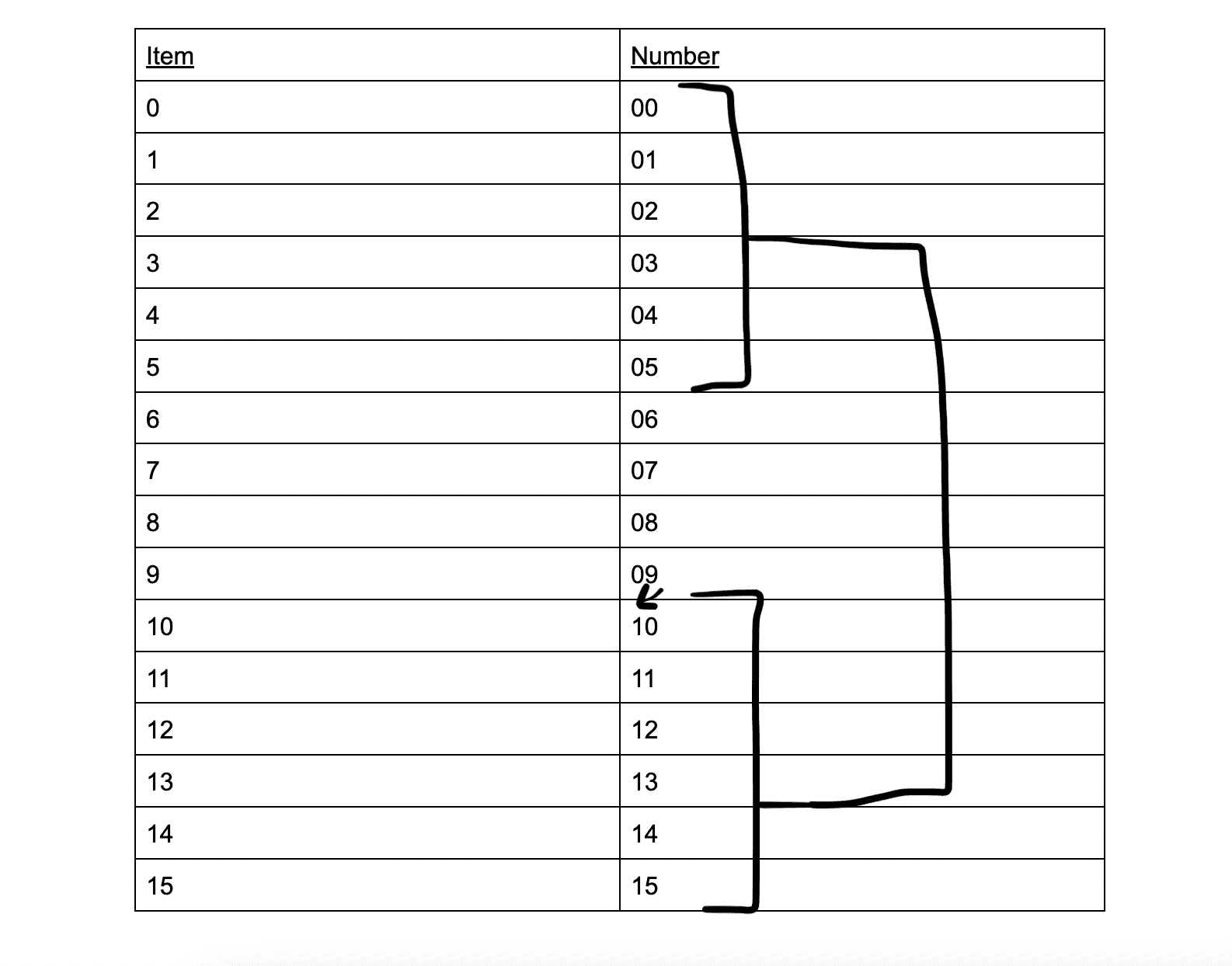
  As you can see above, we just restart counting from zero every time we add a position or place to the left of a number.

• Adding New Digits

  +

  So now you understand that two things matter in seeing the value of a number:

  1. The symbols/digits used to show it
  2. The position or place of those digits

  And you also understand that when we run out of digits in a certain place, we can always add another place/position on the left and restart our counting from there, until we count our number.
  Whenever we add a new position or place when we count a number, it is called rolling over or carrying over a digit

  Now, notice how digits roll/carry over if there are less of them. What if, instead of having the digits 0,1,2,3,4,5,6,7,8, 9 we only have the digits 0,1,2,3,4? Look at the table underneath to see the counting:

  

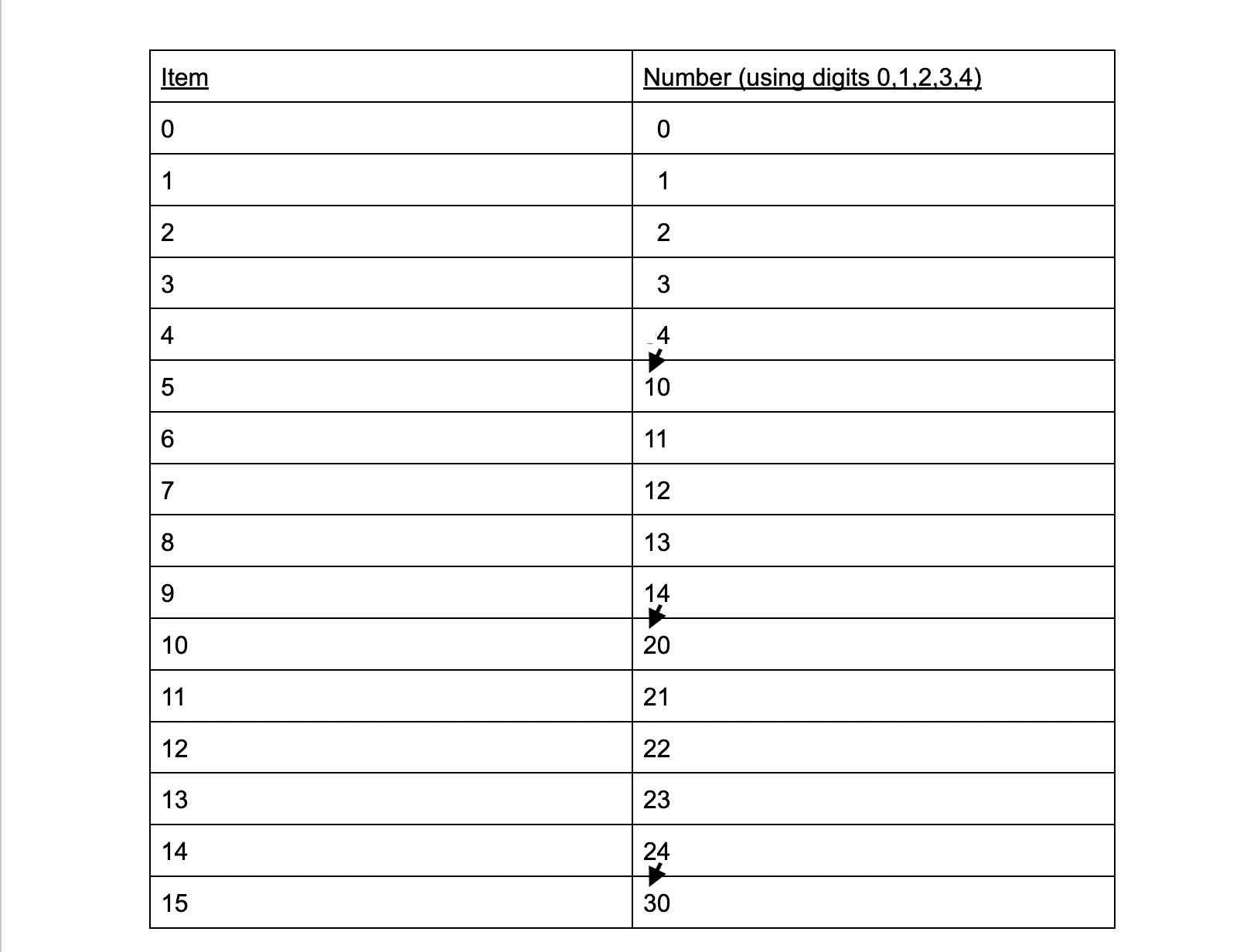
  With 5 digits, the same thing happens when we are counting. We count the digits 0-4 in the first position and, when we don’t have any more digits to put in the first position, add a value to the second position and restart counting.

• Place Value

  +

  We can count any number no matter how many digits we have. The main thing in binary is understanding this counting between digits. But one thing you should know before trying to count in binary is place value. This talks about the value of a number based on its position.

  For example, if I have the digit: 1

  It is considered to be the number “one” because it has no other positions. But for the digits: 10

  It is considered to be the number “ten”, because I have moved the position of the 1.

  So if we wanted to represent 9 in place value, it would look like below. There are 9 digits in the units place and 0 in the tens place.

  Tens Place	Units Place
  0	9

  And if we wanted to represent 10 in “place value”, it would look like below. Here, there are 0 digits in the units place, but there is a 1 in the tens place. Remember, 10 is a bigger number than 09 because of place value:

  Tens Place	Units Place
  1	0

  Using this, there are two main things we can find out about a number.

  1. Any number can be found by multiplying its digit by its place value and adding.

  So in case of 10, that would be:

  1*10 + 0*1 = 10

  Because the one is in the tens place and there is nothing in the units place. Note that the * symbol means multiplication.

  For 9 it would look like:

  0*10 + 1*9 = 9

  And if we have a bigger number like 123, it would look like:

  1*100 + 2*10 + 3*1 = 123

  1. In our number system, the place of each number increases by a factor of 10

  If you noticed above, we move from the units (ones) place, to the tens place, to the hundreds place (and so on) when we are trying to represent a number. So each place is just the last place multiplied by (into) 10.

  Because 10 = 1*10 and 100 = 10*10, so on. That is why we call our number system the base-10 system.

• Binary Place Value

  +

  Binary is just a way of representing a number in a base-2 system instead of base-10.

  In base-10, the place value would look like this:

  100’s Place

  10’s Place

  1’s (Units) Place

  But in binary, the place value looks like this:

  4’s Place

  2’s Place

  1’s Place

  Because in base-10, you need to multiply each place by 10 to get the next one.

  But in base-2 (binary), you need to multiply each place by only 2 to get the next one.

  And since the base is 2, we can only use 2 digits (0 and 1) to represent the number rather than 10 digits in base 10 (0,1,2,3,4,5,6,7,8,9).

  Now that you know what the binary (base-2) system is, it is very easy to convert our base-10 numbers (known as decimal numbers) into binary forms.

  If I had to convert the number 5 into binary form it would look like this:

  4’s Place	2’s Place	1’s Place
  1	0	1

  Because:

  1*4 + 0*2 + 1*1 = 5

  Since 1 is the highest digit in the binary system, the good thing is you can just add the places itself to find the number rather than multiplying.

  So:

  4’s place + 1’s place = 5

  You would put the “1” digit in these places and put the “0” digit in the remaining places. Remember, though, this only works for binary because the highest digit is 1, and 1 multiplied by (into) any number is the number itself. (1*n = n).

  Lastly, what if we wanted to represent the number 8 in binary. If we used the same places (positions) we used to convert 5 into binary, it would look like this:

  4’s Place	2’s Place	1’s Place
  1	1	1

  But, you will see that:

  4 + 2 + 1 = 7

  What this means is that we do not have enough place value to represent the number 8.

  In the base-10 number system, this is like if we have the number 9. To add one more, we need to add another place/position (remember carrying over and rolling over a digit) and put a 1 there to make it 10.

  So in binary form, we will also add another place by multiplying the current place by 2 (since it is base-2).

  Since:

  4*2 = 8

  We will add an 8’s place. We can then represent 8 in binary form as such:

  8’s Place	4’s Place	2’s Place	1’s Place
  1	0	0	0

  What is happening here is that we are carrying over a digit into the new place.

  That is how you can count in binary: if you run out of a place to add a 1 (if your number is too big), add another place. Just like we do in our base-10 number system

• Understanding Binary Counting

  +

  Now we can visualize how counting is done in binary using a place value table that has been used in earlier section. Remember, we only have the digits 0 and 1 to represent each number:

  

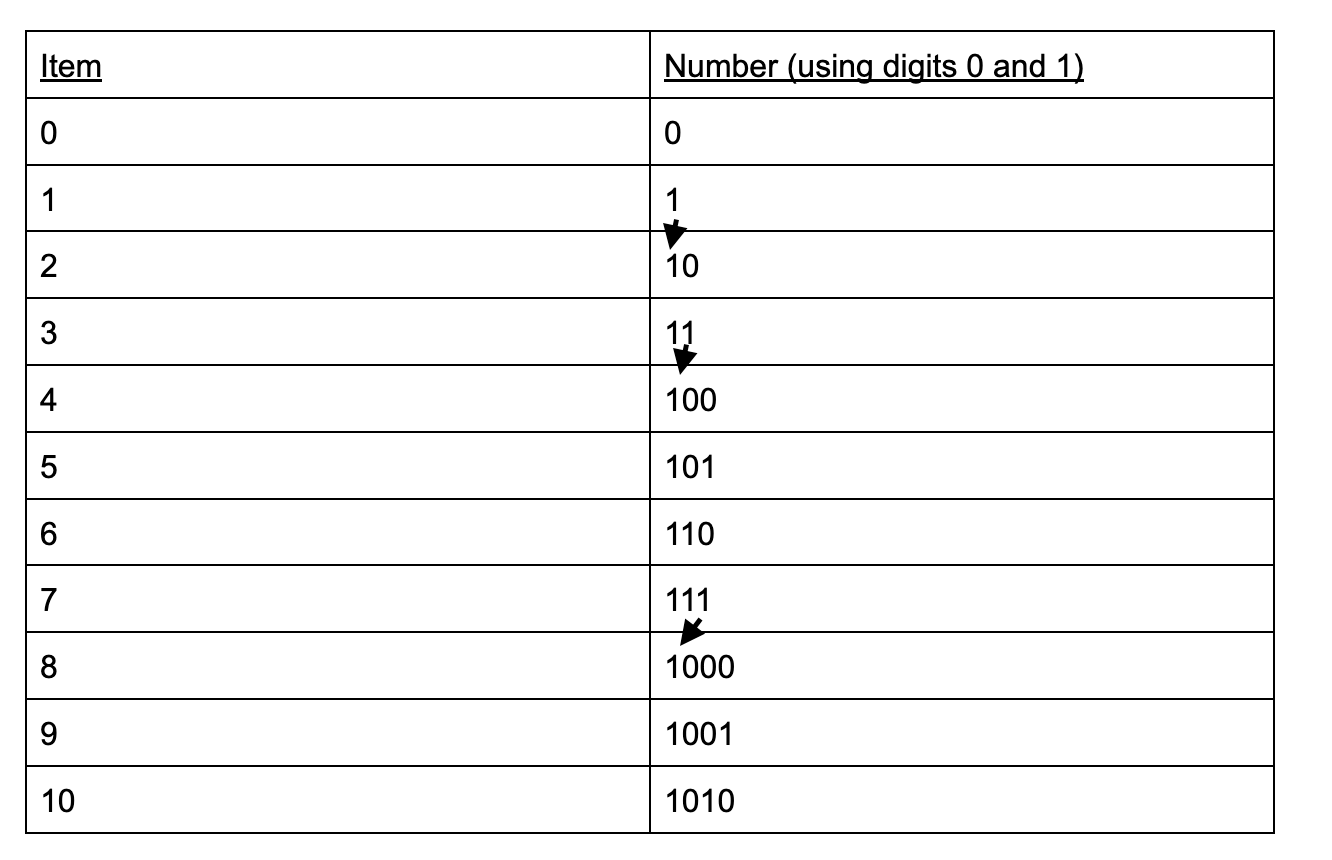
  Again, every time we run out of a position, we carry over to another place and restart our counting.

  In binary, new places are added very fast as there are only two digits (0 and 1). As long as you know how to count by carrying over digits, you will be able to show any number in its binary form.

  Reference Video

• Binary in Computers

  +

  Now that you have learned what the binary number system is, you might be wondering: why is it important in computer science?

  You may have gotten the answer if you were watching the CS50 video but, if not, we will explain a little bit about it here.

  A computer uses binary numbers as a way to represent information about numbers. Inside a computer, there are millions of these tiny switches known as transistors. A larger version of one transistor is shown below:

  

  As said, a transistor is like a switch. So it can be on or off. When a transistor is on, it means that electricity is flowing through it, and electricity stops when it is turned off.

  Computer scientists found a very smart way to link transistors and the binary number system. As said, the binary number system has only two digits (0 and 1).

  So what if each state of the transistor showed a certain digit? If there is no electricity flowing through the transistor, then it will represent the digit 0, but if there is electricity, it will represent the digit 1.

  This means that one transistor represents one place value of the binary system, which can either have digits 0 (off, with no electricity) or 1 (on, with electricity). With many transistors, we can add more places, and can then show very large numbers in binary form on a computer.

  All computers work by storing information in this way, but it gets complicated when they are able to store words and images rather than just numbers. These types of information need more complex versions of binary code, but they work on the same idea of a transistor storing one place of binary.

  Remember, binary (base-2) is chosen to be used by computers because a transistor can only be on or off. There are no more states of the transistor that can be used to show other digits.

• Other Number Systems

  +

  Decimal (base-10) and binary (base-2) number systems are not the only way we can count numbers. There are ways we can represent numbers using base systems from any number. For example, if we had base-3, we could represent a number in one place using three digits (0, 1, and 2). In that case, the places would look like this:

  … 27’s Place

  9’s Place

  3’s Place

  1’s Place

  Because if the base is 3, then we multiply the previous place by 3 to reach the new one

  If we had to represent a number in base-3 (also known as ternary), we would put a 0, 1, 2 in any of these places. For example, this is the number 15 in base-3:

  … 27’s Place	9’s Place	3’s Place	1’s Place
  0	1e	2	0

  Because:

  1*9 + 2*3 = 15

  In this way, we could count using any number system we wish.

  We could keep 4 digits (0,1,2,3) in a base-4 system which has a 1’s place, 4’s place, 16’s place, and a 64’s place.

  We could keep 5 digits (0,1,2,3,4) in a base-5 system which has a 1’s place, 5’s place, 25’s place, and a 125’s place.

  This can go on for number systems with any base. The idea is that you understand that base-2 and base-10 systems are not the only types of ways we can show numbers, there are other ways using the same ideas we learned in the video and explanation above.

• Algorithms Understanding

  +

  Basically, an algorithm is a set of steps you need to take to solve a problem. They are used to solve problems not only in computer science, but everywhere around you. Let me explain:

  Let’s say that I need to buy milk. I can create an algorithm (a set of steps) which would help me solve this problem. For example:

  1. Take money from my parents
  2. Go to the market
  3. Find the milk
  4. Pay for the milk
  5. Come back home

  Just like that ^, we have created an algorithm that tells us how to solve our problem of buying milk.

• If/Else Algorithms

  +

  Now let us look at a more complex algorithm which solves the same problem. What if we buy ghee if there is no milk available at the market? Well, then our algorithm would look like this:

  1. Take money from my parents
  2. Go to the market
  3. If there is milk in the market:
     1. Find the milk
     2. Pay for the milk
  4. Else [if there is no milk available]:
     1. Find the ghee
     2. Pay for the ghee
  5. Come back home

  The above algorithm uses something in programming that is known as an if/else statement (or a conditional). It says that if something is true, then you should perform a certain set of steps, otherwise, you should do other things.

  In this case, if there is milk in the market, then you should buy the milk, otherwise you should buy the ghee.

• Looping

  +

  The last type of algorithm we should look at has something called looping. What if your parents give you a whole list of things to buy from the market. How would you make that into an algorithm? Well, look at the steps below:

  1. Take money from my parents
  2. Go to the market
  3. Read the name of the current item on the shopping list and then:
     1. Find the item
     2. Pay for the item
  4. If you have bought all the items on the list:
     1. Go back home
  5. Else [there are still items on the list remaining]
     1. Repeat step 3 for the next item on the list

  Here’s another way of understanding this algorithm using something called a flowchart:

  

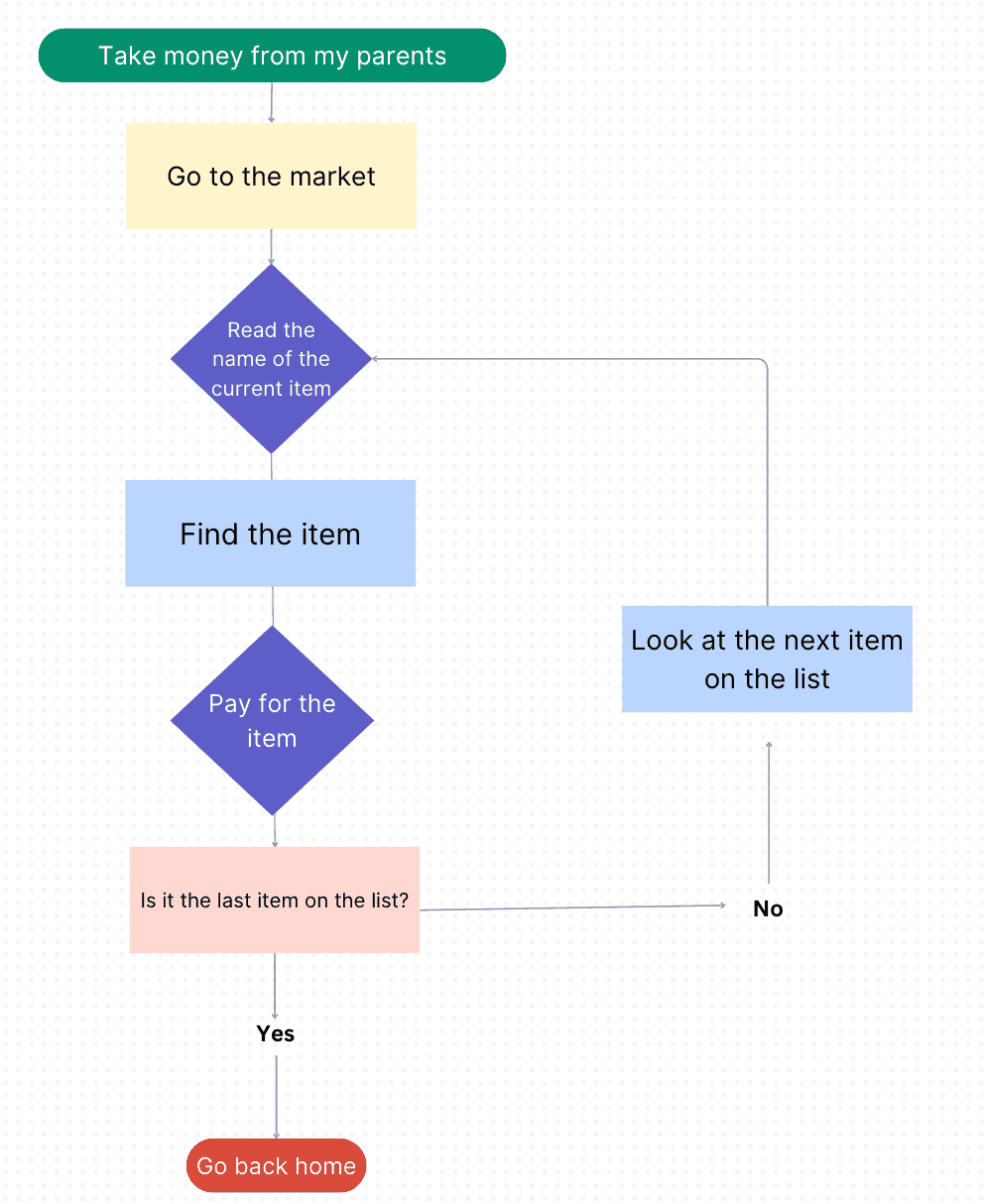
  As you can see in the above chart, we are repeating certain steps over and over again until we reach the last item on our shopping list. This is known as looping and it is a really important part of computer science.

• Video

  +

  Look at another section from the CS50 video to understand how algorithms are written for things like computers. It uses the same ideas we talked about above, so pay attention and see if you can try to find if/else statements or looping.

  Note for the video: a phone book is a book that has a list of people’s names and their phone numbers. All the names are organized alphabetically, where A is written first and Z is written last.

• Analysing Algorithms

  +

  The word analyse means to explain something deeper or in more detail In this section, we will look at how to see which algorithms solve the problem in a faster way, by seeing how many steps they take to work.

  In this section, we will look at how to see which algorithms solve the problem in a faster way, by seeing how many steps they take to work.

  This is the first algorithm we wrote in the last section:

  1. Take money from my parents
  2. Go to the market
  3. Find the milk
  4. Pay for the milk
  5. Come back home

  Looking at the numbers next to each step, we can clearly see that it takes 5 steps to solve the problem.

  But how would we calculate the number of steps a more complex algorithm takes to work. See the algorithm we wrote in the last section which involves looping (where we repeat some steps over and over again):

  1. Take money from my parents
  2. Go to the market
  3. Read the name of the current item on the shopping list and then:
     1. Find the item
     2. Pay for the item
  4. If you have bought all the items on the list:
     1. Go back home
  5. Else [there are still items on the list remaining]
     1. Repeat step 3 for the next item on the list

  To calculate the steps for the above algorithm, we first need to assume one thing:

  Assume that n = the number of items on the shopping list

  The reason this is important is because many steps of the algorithm repeat for all the items on the shopping list. Remember, we are starting from the first item on the shopping list, and can only go home once we have found and bought all the items on the list. So, we end up having to find and buy n items.

• Visualizing Algorithm Analysis

  +

  If you are still confused about this, hopefully the image below makes it more clear. All the steps with tick marks are the ones which are repeated n number of times:

  

  This is only a rough estimate because looping through steps in a computer is a little easier than looping through steps the way we do now. So, pay attention to the concepts being explained here, but do know that there will be some differences when you actually learn computer science.

  Anyways, what do we see in the above image:

  1. There are 5 different steps being repeated n number of times
  2. The four remaining steps will happen only once in our algorithm

  So let’s do the math:

  5*n + 4*1 = 5n + 4

  So as we can see, the number of steps we need to take to buy all the items on the shopping list is 5n+4, where n is the number of items on the list. In computer science language, this is called the time complexity of an algorithm.

  More complex algorithms can have time complexities with terms like n/2 or n-squared rather than just n. You do not need to worry about that for now, though. You should just be able to understand that we can calculate how many steps it takes for an algorithm to solve a problem, not just in computers, but even in the real world.

Introduction

Read the following questions passages carefully and answer the questions based on it.

• The Industrial Revolution

  +

  The Industrial Revolution was a significant turning point in history. It began in the 18th century in Europe and brought about a dramatic shift from hand production to machine manufacturing. This period witnessed the invention of steam engines, the development of factories, and the growth of urban areas. The Industrial Revolution had a profound impact on society, leading to advancements in technology, increased production, and changes in the working conditions of people.

  What was the Industrial Revolution?

  1. A political movement
  2. An artistic period
  3. A scientific theory
  4. A shift from hand production to machine manufacturing

  Which century did the Industrial Revolution start?

  1. 16th century
  2. 17th century
  3. 18th century
  4. 19th century

• About William Shakespeare

  +

  William Shakespeare is widely regarded as one of the greatest playwrights in history. Born in Stratford-upon-Avon, England, in 1564, Shakespeare wrote numerous plays and sonnets that are still performed and studied today. His works, such as "Romeo and Juliet" and "Hamlet," explore themes of love, tragedy, and human nature. Shakespeare's contributions to literature have had a lasting impact on the world of theatre and storytelling.

  Where was William Shakespeare born?

  1. London, England
  2. Paris, France
  3. Stratford-upon-Avon, England
  4. Rome, Italy

  What are some common themes in Shakespeare's works?

  1. Adventure and mystery
  2. Romance and comedy
  3. Love and tragedy
  4. Science fiction and fantasy

• Reading- A Mental Journey

  +

  The Earth's atmosphere is composed of various gases, with nitrogen and oxygen being the most abundant. These gases are essential for supporting life on our planet. In addition to nitrogen and oxygen, the atmosphere also contains trace amounts of carbon dioxide, water vapor, and other gases. The atmosphere plays a crucial role in regulating temperature, protecting against harmful radiation, and facilitating weather patterns.

  What are the most abundant gases in Earth's atmosphere?

  1. Carbon dioxide and oxygen
  2. Nitrogen and hydrogen
  3. Nitrogen and oxygen
  4. Oxygen and helium

  What are some functions of the Earth's atmosphere?

  1. Regulating temperature and facilitating weather patterns
  2. Generating electricity and providing

• Earth’s Atmosphere

  +

  Emma was an avid reader who couldn't resist getting lost in the pages of a good book. Her favourite genre was fantasy, and she loved immersing herself in magical worlds. One day, she stumbled upon a mysterious old bookstore tucked away in a hidden alley. The shopkeeper, a wise-looking man with a long beard, welcomed her warmly and recommended a book that he claimed could transport readers to another realm. Intrigued, Emma purchased the book and hurried home. As she flipped through its pages, she discovered a handwritten note tucked inside, revealing a hidden message. Determined to solve the mystery, Emma embarked on a thrilling quest, unravelling clues and encountering mythical creatures along the way. The enchanted book took her on an unforgettable adventure that surpassed her wildest imagination.

  What genre of books does Emma enjoy reading?

  1. Mystery
  2. Fantasy
  3. Biography
  4. Romance

  How did Emma discover the hidden message in the book?

  1. The shopkeeper told her about it
  2. She found it written on the cover
  3. It was printed at the beginning of the book
  4. It was tucked inside the book

• Emma’s Reading Adventure

  +

  What exercise is to the body, reading is to the mind. There are different purposes for reading. One of them is deriving pleasure. Children reading for their pleasure rarely stop to ask about the words. They want to get on with the story. If the word is important, they can usually make a good guess about what it is. “He drew an arrow from his quiver”. Easy to see that a quiver is some sort of gadget to put arrows in. More complicated words they figure out by meeting them in different contexts. People learn to read well and get a good vocabulary from books, not workbooks or dictionaries. As a kid, I read years ahead of my age, but I never looked up words in dictionaries and didn’t even have a dictionary. In my lifetime, I don’t believe I have looked at even as many as fifty words – neither have most good readers. Most people don’t know how dictionaries are made. Each new dictionary starts from scratch. The company making the dictionary employs thousands of ‘editors’, to whom they give a list of words. The job of the editor is to collect as many examples as possible of the ways in which these words are actually used. They look for the words in books, newspapers, and so forth and every time they find one, they cut out or copy that particular example. Then after reading these examples, they decide ‘from the context’ what the writer in each case had meant by the words. From these, they make definitions. A dictionary, in other words, is a collection of people’s opinions about what words mean as other people use them.

  Q (i). How do children find out meanings when they are reading for pleasure?

  Q (ii). Does the passage suggest that a dictionary is essential for a good vocabulary? Why or why not?

  Q (iii). Write any one step in the process of making a dictionary.

  Q (iv). Define a dictionary in your own words.

  Q (v). Find the phrase in the passage which means ‘calculate/think about until one understands.’

• Kitchen Stories with my Daughter

  +

  Listen to the video carefully and answer the given questions based on it.